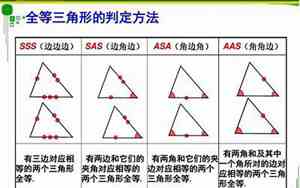
全等三角形的判定是几何学中一个基础但也重要的概念，它意味着两个三角形在形状和大小上完全相同。以下是几种常见的全等三角形判定条件：
1. 边-边-边 (SSS): 如果两个三角形的三边长度相等，那么这两个三角形是全等的。这是通过边的比例和等比性质来判断的。
2. 角-角-边 (ASA) 或角-边-角 (AAS): 如果两个三角形中的两个对应角相等，且其中一个角的对边也相等，或者两个角和其中一个角的对边都相等，那么这两个三角形全等。这个判定法利用了角度和边的对应关系来确定。
3. 直角三角形：如果一个三角形有一个角是90度，且另外两个角和对应边与另一个直角三角形满足上述条件之一（如边对应相等），那么这两个直角三角形也是全等的。
4. 相似三角形的比例关系：如果两个三角形相似，且其中一个三角形的两个对应边与另一个三角形的比例相等，那么这两个三角形是全等的。相似三角形的比例关系包含对应角相等和对应边成比例。
以上是全等三角形判定的几个基本条件，熟练掌握这些方法，可以帮助你在解决几何问题时快速做出准确的判断。
全等三角形的判定方法主要有四种，它们分别是：
1. 边-边-边 (SSS): 简单直观，如果两个三角形的三边长度分别相等，不论三边的顺序如何，这两个三角形都是全等的。这种方法适用于测量或构造完全相同的三角形。
2. 角-角-边 (ASA) 或角-边-角 (AAS): 如果两个三角形有两对对应角相等，并且这两对角之间的边（对应边）也相等，那么这两个三角形是全等的。ASA方法要求两个角度和它们之间的边相等，而AAS则要求两个角度和其中一个角的对边相等。
3. 直角三角形定理 (SAS): 如果一个直角三角形的两个锐角的对边（斜边除外）相等，那么这两个直角三角形全等。这里的SAS不包括直角边。
4. 相似三角形的倍数关系 (HL): 对于直角三角形，如果其中一个直角边（Hypotenuse， 纵坐标）与另一个直角三角形的对应直角边相等，那么这两个直角三角形全等。这是勾股定理的直接应用。
以上每个方法都可能单独或结合使用来确定两个三角形是否全等。在实际问题中，根据给定的条件，选择合适的判定方法是关键。
在教学设计全等三角形的判定方法时，可以按照以下步骤进行：
1. 引入概念：
开始课程时，先回顾三角形的基本概念，然后引入全等三角形的概念，解释全等意味着形状和大小完全相同。
2. 定义与原理讲解：
具体解释SSS（三边对应相等）、ASA（两边夹一角）、AAS（两角夹一边）、SAS（两角及一边对应相等）以及直角三角形的HL判定法。
3. 实例演示：
通过实物模型，动画或者绘图，演示每种判定方法的应用过程，让学生可以直观看到每种方法的实际情况。
4. 互动练习：
设计一些基础的判断问题让学生自己尝试，例如画出全等三角形或者根据条件选择合适的判定方法。
5. 小组合作：
分组让学生互相讲解判定方法，或者解决一些需要利用多种判定方法的问题，促进团队协作和理解深化。
6. 应用题目：
出一些有实际应用场景的题目，让学生用所学知识解决，比如测量、建筑设计等，增强学生的实际应用能力。
7. 总结与巩固：
课堂结束时，总结全等三角形判定的要点，强调每个方法的关键特征，并布置巩固练习。
8. 评估反馈：
收集学生的反馈，了解他们在理解上可能存在的困难，以便调整教学策略。
通过这样的教学设计，可以确保学生不仅理解全等三角形的判定方法，还能熟练运用在实际问题中。同时，互动和实践环节有助于提高他们的动手能力和逻辑思考能力。
全等三角形的八种模型（也称为全等三角形的几种特殊情况）是指特定形状或性质的三角形，它们在一定条件下可以推断彼此全等。以下是一些典型的全等三角形模型及其应用的例题：
1. 直角三角形全等模型：
例题：一个直角三角形的斜边长是10cm，另一小直角三角形的斜边与它相等。证明这两个直角三角形全等。
2. 等腰三角形模型：
例题：已知两个等腰三角形，一边长分别是5cm和4cm，底角相等，证明这两个三角形全等。
3. 等边三角形模型：
例题：两个等边三角形，但没有长度信息，只有三个角度都为60度，判断它们是否全等。
4. 顶角-底边-底角 (ASA) 或顶角-底边-对应角 (AAS) 模型：
例题：在一个三角形中，两个角度分别是60度和80度，和它们对应的那条边长8cm，另一个三角形有相同的两个角度，边长也相等，证明这两个三角形全等。
5. ASA或AAS模型：
例题：已知一个三角形的两个角和夹角对边长，另一个三角形有相同的两个角和夹边，证明它们全等。
6. SAS模型：
例题：一个三角形两个锐角的对边分别是6cm和8cm，另一个三角形的两个锐角的对边也恰好相等，证明这两个三角形全等。
7. 直角三角形的直角边-对角线 (SAS)：
例题：已知一个直角三角形，一条直角边为5cm，另一条直角边对应着的对角线长度也是5cm，证明直角三角形全等。
8. 相似三角形的比例关系 (相似但不全等)：
例题：两个三角形相似，其中一个三角形的两个边长分别为3cm和4cm，另一个三角形的对应边长分别是6cm和8cm，求证它们是倍数关系。
通过解决这类例题，学生可以熟练掌握全等三角形的各种判定方法，并能灵活运用到实际问题的解题中。
记得在使用他人的模板时，确保其版权允许个人或教育用途，并适当修改以适应你的教学需求。
实际上，全等三角形的判定条件被总结为六种，但其中一种情况是“边-边-边 (SSS)”，也就是三边对应相等，这被视为一种。所以，准确的六种判定条件是：
1. 边-边-边 (SSS): 当两个三角形的三边长度都相等时，这两个三角形全等。
2. 角-角-边 (ASA): 若两个三角形有两对对应角相等，并且这两个角的夹边也相等，它们是全等的。
3. 角-边-角 (AAS): 同样，如果两个角相等，且其中一个角的对边也相等，那么这两个三角形全等。
4. 直角三角形的HL定理 (HL): 在直角三角形中，如果有一条直角边与另一直角三角形的对应直角边相等，那么这两个直角三角形全等。
5. SAS (两边夹一角): 两个三角形有一对对应边相等且夹角相等，那么它们全等。
6. SSA (一边对两边): 这种情况通常不被视为有效的全等判定条件，因为存在一个假同角三角形的误解，即两边对两角，不能保证全等，除非另外还知道一个边的具体尺寸。
每一种方法都有其特定的适用性，教师在教学时会根据具体情况和学生的理解水平选择最适合的判定条件。
猜你喜欢
