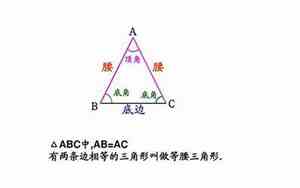
在一个等腰三角形中，如果两个底角相等，那么它们的角度是相等的。由于三角形内角和为180度，如果底角是相等的，那么每个底角会是180度除以2，即每个底角是90度。剩下的那个角，也就是顶角，因为是两个底角的和，所以顶角也是180度 - 2 * 90度 = 0度。但是，在常规情况下，一个等腰三角形的顶角是两个底角度数的平均值，即90度，除非它是一个特殊的等边三角形（所有角都是60度）。
对于直角三角形，其名称来源于其中一个角是90度，这个角被称为直角。直角三角形的另外两个角的和必须是90度，其中一个角可以是任意锐角（小于90度），另一个角则是对应的补角（即90度减去那个锐角）。例如，一个常见的直角三角形，如3-4-5三角形，其中两个锐角分别是30度和60度。
等腰三角形的周长公式并不复杂，它是三条边长的总和。假设等腰三角形的两腰（即两个相等的边）长度为a，底边为b，那么周长P可以表示为：
\[ P = a + a + b \]
由于等腰三角形有两条边相等，所以这里的a实际上会被计算两次。如果已知腰长和底长，可以直接将它们相加。如果只知道腰长和腰长，或者只知道底边和腰长，那么需要根据具体信息进行计算。例如，如果腰长是a，底边是b：
如果只知道腰长，周长就是 \(P = 2a + b\)
如果只知道底边，假设底边是b，那么周长就是 \(P = 2a + b\)，其中a需要根据题目给出的关系计算（通常等腰三角形的两个腰是相等的）。
请提供更具体的信息，以便给出准确的计算。
直角三角形的三个角总和为180度，其中最重要的一点是有一个角是90度，这个角被称为直角。在标准的直角三角形中，剩下的两个角是两个锐角，且其中一个角（通常较小的）被称为余角（通常记为α），另一个较大的角被称为补角（记为β）。这两个锐角的度数可以是任意的，但为了满足三角形内角和为90度，它们必须满足以下关系：
\[ 90° (直角) = α + β \]
如果α是较小的那个锐角，那么β就是直角减去α，即：
\[ β = 90° - α \]
反之，如果β是较小的角，α则为：
\[ α = 90° - β \]
常见的直角三角形，比如3-4-5三角形，其中两个锐角是30°和60°，因为30°角对边是斜边的一半，60°角对边是斜边的根号三倍。但这不是唯一的组合，直角三角形的角有多种可能的配对方式。
是的，等腰三角形的两个底角是相等的。这个性质是等腰三角形的基本特征之一。在等腰三角形中，两条边（腰）是相等的，这两条边所夹的两个角（底角）也是相等的。由于三角形内角和为180度，所以两个相等的底角加上顶角的和也是180度。等腰三角形的对称性使得它有两个完全相同的底角。如果没有其他特别说明，等腰三角形的两个底角总是相等的。
等腰三角形的角有以下特点：
1. 两个底角相等：等腰三角形的两个底边（即两条等长的边）所对应的角是相等的，这个性质叫做底角相等。
2. 两个相等的角加上第三个角的度数等于180度：因为三角形的内角和为180度，所以等腰三角形的两个底角之和等于顶角的度数。
3. 顶角可以是锐角、直角或钝角：具体取决于底角的大小。如果底角为60度（等边三角形的情况），那么顶角也是60度，是等边三角形。如果底角小于60度，则顶角大于60度且小于120度，是锐角；若底角为90度，则顶角为0度，是直角；若底角小于45度，那么顶角大于135度，是钝角。
4. 对称性：等腰三角形至少有一条轴对称，这意味着它可以通过这条轴平分为两个全等的三角形，这条轴就是通过底边中点的轴，对应于底角的对称轴。
5. 如果只知道腰和底，可能存在两个不同的等腰三角形：比如腰长为a，底边为b，那么a可以是b的两倍，也可以是b的一半，取决于其他条件，如角度信息。
这些特点使得等腰三角形在几何学中有所区别，它们的对称性和角度关系在解决相关问题时具有重要作用。
等腰三角形中有两条边是相等的，通常称为腰，而另一条边则是底边（base或apothem），与腰不同的那条边称为底边（如果它不是最长的边）。等腰三角形的三边关系可以有如下几种：
1. 两腰相等：这是等腰三角形的定义，所以如果两条边相等，那么它们就是等腰三角形的两腰。
2. 底边与腰的关系：底边通常不与腰相等，除非它是等边三角形（所有边都相等），在这种情况下，三条边长度相等。
3. 三角形内角和：等腰三角形的三个角的和等于180度。若底角为一个确定的度数，那么顶角可以通过180度减去两个底角来计算。
4. 斜边与腰的关系：若等腰三角形内包含一个直角，则底边（直角边）和另外一条腰可以形成一个直角三角形，根据勾股定理，底边的平方加腰的平方等于斜边的平方。
5. 相似三角形：等腰三角形可以与其他三角形互为相似三角形，如果它们的对应角相等，那么它们的比例关系是固定的。
等腰三角形的三边关系主要体现在边长的相等性和内角的分配上，这种结构使得其具有独特的几何性质。
等腰三角形是一种特殊的三角形，它具有以下性质：
1. 两腰相等：等腰三角形的两条边长相等，通常称为腰。这是等腰三角形最重要的特征。
2. 底角相等：等腰三角形的两个底角（与腰相对的角）是相等的。这是等腰三角形的对称性体现。
3. 顶角的对称性：等腰三角形的顶点对称于底边中点，形成轴对称性。
4. 相似三角形：如果等腰三角形的两边和另一个三角形的两边对应相等，则这两个三角形相似。
5. 内角和：等腰三角形的三个内角之和为180度，且两个底角的和为顶角的两倍。
6. 根据直角三角形的定义：如果等腰三角形中有一个直角，那么它是等腰直角三角形，其中一个底角是45度，另一个底角也是45度，顶角是90度。
7. 勾股定理应用：对于等腰三角形内的直角三角形，勾股定理依然成立，即两腰的平方和等于底边的平方。
8. 等腰三角形的高线和中线相等：底边上的高线（垂直于底边的线）等于底边的一半，同时中线（连接顶点到底边中点的线）也等于腰的一半。
这些性质使得等腰三角形在几何证明和计算中具有方便之处，对理解和解决相关问题非常有帮助。
猜你喜欢
